LOGICA DE ESCALERA

LECCION 8

LOGICA DE ESCALERA BASICA

LENGUAJES DE PROGRAMACION

Existen varias opciones en lenguajes de programación de las cuales el usuario puede decidir cual se adapta de mejor manera a su aplicación o su estilo de diseño:

• Lógica de escalera
• Diagrama de bloque de funciones
• Texto estructurado

LOGICA DE ESCALERA

Es  un lenguaje de programación que utiliza símbolos semejantes a los usados en diagramas de relé eléctricos por electricistas:

• Escalones
• Instrucciones
• Ramas

ESCALONES

Las instrucciones dentro de una lógica de escalera son acomodadas de acuerdo a la secuencia en la que intervienen en un proceso; de manera mas clara se dirá que se leen de izquierda a derecha y de arriba hacia abajo. Se debe considerar lo siguiente:

• Los escalones son escaneados del 0 al número mayor
• Los escalones no pueden estar vacios
• El último escalón es la instrucción end. No contiene ninguna instrucción.

INSTRUCCIONES

Las instrucciones son comandos definidos operaciones/evaluaciones realizados por el controlador:

• Instrucciones de entrada: evalúan datos en un controlador
• Instrucciones de salida: colocan datos en un controlador

Existen algunas reglas para colocar las instrucciones en un renglón:

ü  Un escalón puede o no tener instrucciones de entrada, pero debe contener al menos una instrucción de salida

ü  La ultima instrucción en un escalón debe ser una instrucción de salida

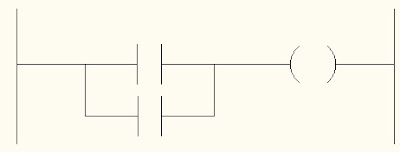
RAMAS

Las ramas son usadas como rutas alternativas para leer instrucciones de entrada y salida:

Las ramas pueden tener más de un nivel y pueden incluir dos tipos:

• Rama paralela: una rama que tiene el mismo punto de entrada y salida como la rama ubicada por debajo
• Rama anidada: una rama que empieza y finaliza dentro de otra rama.

ü  Las ramas son leídas de izquierda a derecha y de arriba hacia abajo

ü  Una rama debe iniciar y terminar en el mismo nivel

           

Las ramas paralelas son evaluadas de manera más rápida que las anidadas

CONTINUIDAD LOGICA

La continuidad lógica hace referencia a una situación donde las instrucciones de entrada permiten una ruta de señal “verdadera” hacia las instrucciones de salida.

ü  Si A es verdadera entonces D es verdadera.

ü  Si A es falsa entonces D es falsa.

Existen tres combinaciones posibles de entradas para determinar la continuidad lógica:

• AND
• OR
• AND junto con OR

Si A y B son verdaderas entonces D es verdadera (AND).

Si A o B son verdaderas entonces D es verdadera (OR).

Si A y C son verdaderas o B y C son verdaderas entonces D es verdadera (AND con OR).

COMBINACIONES DE SALIDAS

Salida incondicional

Múltiples salidas

Salidas con entradas separadas